Question

How do you multiply imaginary numbers? For example (2i)^4 and 2i•8i?

Answer 1

The process of multiplying complex numbers is very similar when we multiply two binomials.

The only difference is the introduction of the expression:

`\sqrt[]{-1}\text{ = i}`

For example,

Multiply 2i by 8i

`\begin{gathered} 2i\text{ }*\text{ 8i = 2}*\text{ 8}*\text{ i}*\text{ i} \\ =\text{ 16}* i^2 \\ =\text{ 16 }*\text{ -1} \\ =\text{ -}16 \end{gathered}`

We must remember the following when multiplying imaginary numbers:

`\begin{gathered} \sqrt[]{-1}\text{ = i} \\ i^2\text{ = -1} \end{gathered}`

Let's work on another example:

(2i)^4:

`\begin{gathered} =(2i)^4 \\ =\text{ 2i }*\text{ 2i }*\text{ 2i }*\text{ 2i} \\ =\text{ 2}*2*2*2\text{ }* i* i* i* i \\ =\text{ 16 }* i^2\text{ }* i^2 \\ =\text{ 16 }*\text{ -1}*-1 \\ =\text{ 16} \end{gathered}`

Remember that:

`\begin{gathered} i^2\text{ = -1} \\ i^3=i^2\text{ }*\text{ i} \\ =\text{ -i} \\ i^4=i^2\text{ }* i^2 \\ =\text{ -1 }*\text{ -1} \\ =\text{ 1} \end{gathered}`

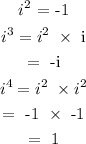
Anytime we raise i to any power, the result changes depending on the value of the power. We can obtain the result by evaluating the terms as shown above.