Notice that f(x) corresponds to a parabola that opens upwards on the plane; therefore, its only critical point is a minimum. Solve f'(x)=0 to find the minimum value of f(x), as shown below
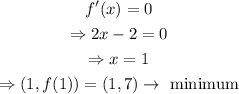
On the other hand, from the image, the maximum value of g(x) is at (3,12).
Therefore, the difference between the maximum value of g(x) and the minimum value of f(x) is
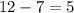
The answer is 5.