Question

Identifying parallel and perpendicular lines from equationsThe equations of three lines are given below.Line 1: 2y =5x+3Line 2: 10x + 4y=42Line 3: y = 2x+5For each pair of lines, determine whether they are parallel, perpendicular, or neither.Line 1 and Line 2: O Parallel Perpendicular ONeitherx?Line 1 and Line 3: O Parallel O Perpendicular O NeitherLine 2 and Line 3:Parallel Perpendicular Neither

Answer 1

Parallel lines have equal slope.

Perpendicular lines have slopes that are negative reciprocals of each other.

Now, let us find the slope of each line.

Remember, the line's equation expression is :

`y=mx+b`

Now,

Line 1:

`\begin{gathered} 2y=5x+3 \\ y=(5)/(2)x+(3)/(2) \end{gathered}`

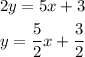
Slope if 5/2

Line 2:

`\begin{gathered} 10x+4y=4 \\ 4y=-10x+4 \\ y=-(10)/(4)x+1 \end{gathered}`

SLope is -10/4, or -5/2

Line 3:

y = 2/5x + 5

We don't have to rearrange, so the slope is 2/5

Now,

Answer choices

LIne 1 and Line 3 = neither (slope of 2/5 and 5/2 is neither same nor negative reciprocal)

Line 2 and Line 3 = Perpendicular. THey are exactly the NEGATIVE RECIPROCAL

Line 1 and Line 2 = they are same magnitude but different sign. Doesn't make sence.

SO, they are neighther.