Question

A rectangular playground is to be fenced off and divided in two by another fence parallel to one side of the playground. Four hundred feet of fencing is used. Find the dimensions of the playground that maximize the total enclosed area. What is the maximum area?

Answer 1

Answer:

The maximum area is

`100*33(1)/(3)ft^2`

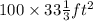
Step-by-step explanation:

Let the playground be demonstrated as follows:

The perimeter of a rectangle is:

P = 2x + 3y

This is given as 400, so

2x + 3y = 400

y = (400 - 2x)/3

Area = x * y

= x * (400 - 2x)/3

`A=-(2)/(3)x^2+(400)/(3)x`

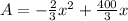
Maximum is dA/dx = 0

`\begin{gathered} -(4)/(3)x+(400)/(3)=0 \\ \\ -4x+400=0 \\ x=(400)/(4)=100 \end{gathered}`

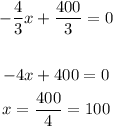
2x + 3y = 400

2(100) + 3y = 400

3y = 400 - 200

3y = 100

y = 100/3 = 33 1/3

The maximum area is 100 * 33 1/3