Question

Is (x-3) a factor of f(x) = x^2 - 32?

Answer 1

`No`

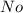
Step-by-step explanation:

Here, we want to use the factor theorem to check if the given linear expression is a factor of the binomial

Now, according to the factor theorem, a factor of a polynomial would leave no remainder when divided by it

Mathematically, it means when we substitute the factor value into the polynomial, it is expected that the remainder is zero is the substituted is a factor of the polynomial

We set x-2 to zero:

`\begin{gathered} \text{ x-2 = 0} \\ x\text{ = 2} \end{gathered}`

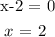
Now, we substitute 2 into the polynomial as follows:

`f(2)\text{ = }2^2-32\text{ = 4-32 = -28}`

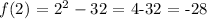
There is a remainder of -28 and thus, the linear factor is not a factor of the binomial