ANSWER
Jesse's average speed to her parent's house is 72 mph and her average speed from her parent's house is 56 mph
Step-by-step explanation
Let Jesse's average speed on her way home be x mph.
This implies that her average speed on her way to her parent's house is (x + 16) mph.
The average speed is given by:
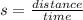
This implies that time is:
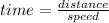
Hence, the total time spent by Jesse is:

We are given that the total time Jesse spent driving is 4 hours. This implies that:
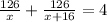
Solve for x in the equation above:
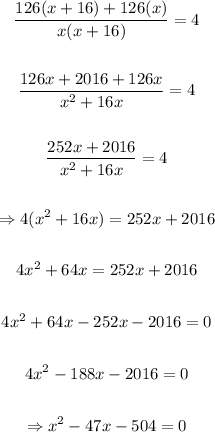
Solve for x by factorizing:
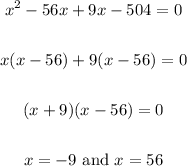
Since speed cannot be negative, it implies that Jesse's average speed on her way home from her parent's house is:
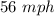
And her average speed on her way to her parent's house is:
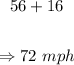
That is the answer.