Question

6#Suppose that IQ scores in one region are normally distributed with a standard deviation of 17. Suppose also that exactly 58% of the individuals from this region have IQ scores of greater than 100 (and that 42% do not). What is the mean IQ score for this region? Carry your intermediate computations to at least four decimal places. Round your answer to at least one decimal place.

Answer 1

103.4

Explanation:

Given:

Standard deviation (σ) = 17

x = 100

The probability is 42%, that is 0.42, we look for this value in the normal table to determine the value of z as follows:

z = -0.2

Knowing that value we can calculate the mean, just like this:

`\begin{gathered} z=(x-\mu)/(\sigma) \\ \\ \text{ We replacing:} \\ \\ -0.2=(100-\mu)/(17) \\ \\ 100-\mu=-0.2\cdot17 \\ \\ \mu=100+0.2\cdot17 \\ \\ μ=103.4 \end{gathered}`

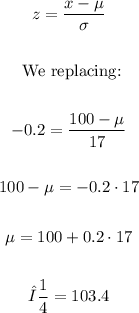
The mean is equal to 103.4