Question

Find GH. BC 19 GH 9x - 3 FE 5х + 1 option A: 2 option B: 6 option C: 15. option D: 51

Answer 1

Since FE and BC are given to be parallel, the figure BCEF is a trapezium.

The line GF divides the sides BF and CE equally. Hence, we can say that GH is parallel to side FE and BC.

Hence, the trapeziums BCHG and FEHG are similar.

Hence, the ratio between sides can be expressed as,

`\frac{\text{BC}}{GH}=(GH)/(FE)`
`\begin{gathered} (19)/(9x-3)=(9x-3)/(5x+1) \\ 95x+19=(9x-3)^2 \\ 95x+19=81x^2-2*3*9x+9 \\ 95x+19=81x^2-54x+9 \end{gathered}`
`0=81x^2-149x-10`

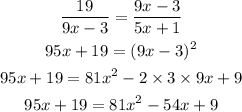
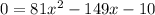
Using discriminant method, the equation can be solved as,

`\begin{gathered} x=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a} \\ x=\frac{-(-149)\pm\sqrt[]{(-149)^2-4*81*(-10)}}{2*81} \end{gathered}`

The positive solution to the equation is x≈2.

So,

`\begin{gathered} GH=9*2-3 \\ =15 \end{gathered}`

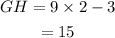
Hence, GH=15.