We are given the following quadratic inequality.
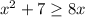
Let us convert it into quadratic form and then factorize the equation
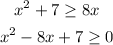
So now we need two numbers such that their sum is equal to -8 and their product is equal to 7.
How about -7 and -1 ?
Sum = -7 - 1 = -8
Product = -7*-1 = 7
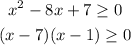
Now there are few possible cases
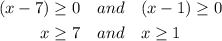
Since x => 1 meets the requirement of x => 7 so we take x => 1 form here.
The other possible case is
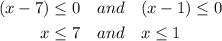
Since x <= 7 meets the requirement of x <= 1 so we take x <= 7 form here.
So the solution becomes

Finally, the solution in interval notation is written as
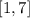
We use brackets for closed intervals (less, greater or equal than cases)
We use parenthesis for open intervals (less, greater than cases)