Answer:
B. -6/7 x - 16/3
Explanation:
The equation of a line in slope-intercept form is given by

where m = slope and b = y-intercept.
First, let us find the equation for line J.
We are told that the y-intercept of line J is -15, meaning J passes through (0, -15). Furthermore, we are told that J also passes through (6, -8). Therefore, the slope of the line is given by
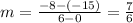
Therefore, the equation for J is
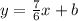
Now we know that the y-intercept for J is -15. Therefore, b = -15 and so the above equation gives
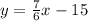
Now, what is a line K that is perpendicular to the above line?
Here we remind ourselves that if we have an equation of the form y = mx + b, then the equation for a perpendicular line is given by
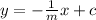
where c is a y-intercept that can be different from b.
Now in our case m = 7/6; therefore, the equation for the perpendicular line
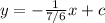
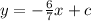
Now, what is the value of c, the y-intercept?
We are told that the line K passes through the point (-7, 2/3); therefore, putting x = -7 and y = 2/3 into the above equation gives
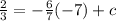
which simplifies to give

subtracting 6 from both sides gives
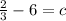

with the value of c in hand, we can now write the equation for the line K.
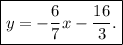
which is our answer!
Looking at the answer choices we see that choice D gives the equation we found above.
Therefore, choice D is the correct answer.