Question

The scale factor of two similar spheres is 1:3. The ratio of their areas isvolumes is1:31:61:9 :: 1:27:: 1:81The ratio of thei

Answer 1

.Step-by-step explanation

We are given the scale factor of two similar spheres as 1 : 3.

We are required to determine the ratio of their areas and volumes.

We know that when you're working with scale factors, you square the scale factor to determine the area of the new figure Thus:

`\begin{gathered} Ratio\text{ }of\text{ }their\text{ }areas=(1:3)^2=((1)/(3))^2=(1)/(9) \\ Ratio\text{ }of\text{ }their\text{ }areas=1:9 \end{gathered}`

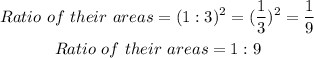
Also, the change in volume is equal to the scale factor cubed. Thus:

`\begin{gathered} Ratio\text{ }of\text{ }their\text{ }volumes=(1:3)^3=((1)/(3))^3=(1)/(27) \\ Ratio\text{ }of\text{ }their\text{ }volumes=1:27 \end{gathered}`

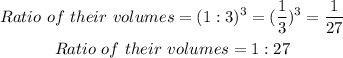
Hence, the answers are:

`\begin{gathered} Ratio\text{ }of\text{ }their\text{ }areas=1:9 \\ \\ Ratio\text{ }of\text{ }their\text{ }volumes=1:27 \end{gathered}`