Question

If a cone has the same radius and height as a cylinder, the volume of the cone is the volume of the cylinder. If a cylinder and a sphere have the same radius and the cylinder’s height is twice its radius, then the volume of the sphere is the volume of the cylinder

Answer 1

Answer: one third

two thirds

Explanation:

If a cone has the same radius and height as a cylinder, the volume of the cone is one-third the volume of the cylinder. If a cylinder and a sphere have the same radius and the cylinder’s height is twice its radius, then the volume of the sphere is two-thirds the volume of the cylinder.

Answer 2

We are given a cone that has the same radius and height as a cylinder. The volume of a cone is given by:

`V_c=(1)/(3)\pi r^2h`

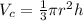
The volume of a cylinder is:

`V_c=\pi r^2h`

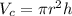
Therefore, the volume of the cone is one-third the volume of the cylinder.

We are also told that a cylinder and a sphere have the same radius and the cylinder’s height is twice its radius.

The volume of a sphere is:

`V_(sp)=(4)/(3)\pi r^3`

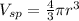
The volume of a cylinder is:

`V_c=(1)/(3)\pi r^2h`

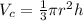
We have that:

`h=2r`

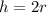
Replacing in the formula for the volume of the cylinder:

`V_c=(1)/(3)\pi r^2(2r)`

Simplifying:

`V_c=(2)/(3)\pi r^3`

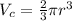
Multiplying by 2:

`2V_c=(4)/(3)\pi r^3`

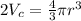
Therefore:

`2V_c=V_(sp)`

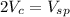
Therefore, the volume of the sphere is twice the volume of the cylinder.