Given data:
The given vertices of the parallelogram are K(2, 7), L(6, 12), M(13, 13) and N(9, 8).
In parallelogram opposite sides are equal and parallel.
![\begin{gathered} KL=\sqrt[]{(6-2)^2+(12-7)^2} \\ =\sqrt[]{4^2+5^2} \\ =\sqrt[]{16+25} \\ =\sqrt[]{41} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/high-school/vcy701yjm0zljd5ct02930l3gwc495aggh.png)
The slope of KL is,
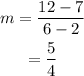
The measuremment of the side MN is,
![\begin{gathered} MN=\sqrt[]{(9-13)^2+(8-13)^2} \\ =\sqrt[]{16+25} \\ =\sqrt[]{41} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/high-school/3ysyckyhx2xycth55vv7khq31ash72sioc.png)
The slope of the MN is,
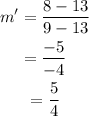
The LM length is,
![\begin{gathered} LM=\sqrt[]{(13-6)^2+(13-12)^2} \\ =\sqrt[]{49+1} \\ =\sqrt[]{50} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/high-school/h8r79alyn6fvnsz7gxa0grifbip1h02veh.png)
The slope of LM is,
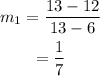
The length NK is,
![\begin{gathered} NK=\sqrt[]{(2-9)^2+(7-8)^2} \\ =\sqrt[]{49+1} \\ =\sqrt[]{50} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/high-school/f0o3phr8f3zift2l8i5fgxhv42bc7rm79b.png)
The slope of NK is,
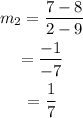
As, the opposite sides are equal and parallel, so the given quadrilaterl KLMN is parallelogram.
Thus, Yes it is parallelogram, so first option is correct.