Answer:
f(x) = 6x + 8
Explanation:
Pre-Solving
We are given the points (7,50), and (1,14).
We want to write a function of the line that passes through these points.
The form of a linear function is f(x) = mx+b, where m is the slope and b is the y intercept.
**Note that f(x) acts as the same as y, so when doing calculations, we can use y instead of f(x), and then substitute f(x) as y at the end.
Solving
Slope
Let's first find the slope of the function.
The slope (m) can be found using the formula
 , where
, where
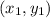 and
and
 are points.
are points.
We can label the values of the points to avoid any confusion and mistakes.
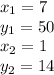
Substitute the values.

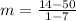
Subtract.

Divide.
m = 6
The slope is 6.
y intercept
We can substitute 6 as m in y = mx+b
y = 6x + b
Now we need to find b.
As the equation passes through the points (7, 50) and (1, 14), we can use either point to help solve for b.
Let's take (1, 14) for example.
Substitute 1 as x and 14 as y.
14 = 6(1) + b
Multiply
14 = 6 + b
Subtract 6 from both sides
8 = b
Substitute b as 8.
y = 6x + 8
Final answer
Substitute f(x) for y.
f(x) = 6x + 8