Question

Solve each system by graphing. If the lines are parallel, write no solution. If the lines coincident, write infinitely many solutions.

Answer 1

No Solution

Step-by-step explanation:

Given the system of equations:

`\begin{gathered} y-2x=4 \\ y=5+2x \end{gathered}`

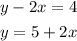
First, graph each equation using the x and y-intercepts.

Equation 1

`\begin{gathered} y-2x=4 \\ \text{When }x=0,y=4\implies\text{Point (0,4)} \\ \text{When y}=0,x=-2\implies\text{Point (-2,0)} \end{gathered}`

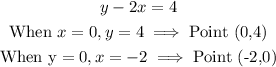
Join the points (0,4) and (-2,0) as done below:

Equation 2

`\begin{gathered} y=5+2x \\ \text{When }x=0,y=5\implies\text{Point (0,5)} \\ \text{When y}=0,x=-2.5\implies\text{Point (-2.5, 0)} \end{gathered}`

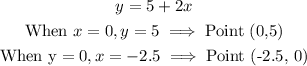
Join the points (0,5) and (-2.5, 0) as done below:

We observe that the two lines are parallel.

Therefore, the system of equations has No Solution.