Question

A herd of 23 white-tailed deer is introduced to a coastal island where there had been no deer before. Their population is predicted to increase according toA=276/1+11e^-0.35t(a) How many deer will be present after 3 years? Round your answer to the nearest whole number.(b) What is the carrying capacity for this model?(c) How many years will it take for the herd to grow to 50 deer? Round your answer to the nearest whole number.

Answer 1

c). Two and half years (2.5 years).

Step-by-step explanation

Given:

`A\text{ = }\frac{276}{1\text{ + 11}e^(-0.35t)}`

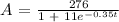
Desired Outcome:

The number of years it will take for the herd to grow to 50 deer

Determine time 't'

`\begin{gathered} 50\text{ = }\frac{276}{1\text{ + 11}e^(-0.35t)} \\ 50(1\text{ + 11}e^(-0.35t))\text{ = 276} \\ 50\text{ + 550}e^(-0.35t)\text{ = 276} \\ 550e^(-0.35t)\text{ = 276 - 50} \\ e^{-0.35t\text{ }}\text{ = }(226)/(550) \\ e^(-0.35t)\text{ = 0.4109} \\ \ln e^(-0.35t)\text{ = }\ln(0.4109) \\ -0.35t\text{ = -0.8894} \\ t\text{ = }(-0.8894)/(-0.35) \\ t\text{ = 2.5 } \\ t\text{ = 2}(1)/(2)\text{ years} \end{gathered}`

Hence, it will take two and half (2.5) years for the herd to grow to 50 deer.