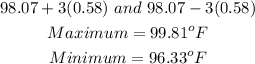Question

According to a random sample taken at 12 A.M., body temperatures of healthy adults have a bell-shaped distribution with a mean of 98.07°F and a standard deviation of 0.58°F. Using Chebyshev's theorem, what do we know about the percentage of healthy adults with body temperatures that are within 3 standard deviations of the mean? What are the minimum and maximum possible body temperatures that are within 3 standard deviations of the mean?

Answer 1

SOLUTION;

Using Chebyshev's theorem the percentage of healthy adults with body temperatures that are within 3 standard deviations of the​ mean make up at least 89% of the population.

Thus;

The maximum and minimum possible body temperatures that are within 3 standard deviations of the​ mean are;

`\begin{gathered} 98.07+3(0.58)\text{ }and\text{ }98.07-3(0.58) \\ Maximum=99.81^oF \\ Minimum=96.33^oF \end{gathered}`