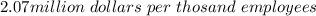Question

Refer to Question 16. How fast is the profit increasing when there are only 900 employees (x = 0.9)? Again,round to two decimal places and make sure to include the correct units.Edit View Insert Format Tools TableQuestion 16 is the image

Answer 1

We are given the function

`P(x)=ln(4x+1)+3x-x^2`

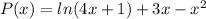
We want to find how fast is the profit increasing when there are only 900 employees (x = 0.9).

To do that, we will have to differentiate P(x) with respect to x and then substitute the value of x = 0.9

Note

`\begin{gathered} Given=ln(4x+1) \\ Differentiate=(4)/(4x+1) \\ \\ Given=3x \\ Differentiate=3 \\ \\ Given=x^2 \\ Differentiate=2x \end{gathered}`

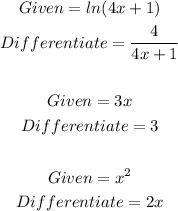
Now, we differentiate

`\begin{gathered} P(x)=ln(4x+1)+3x-x^(2) \\ B\text{y differentiating} \\ P^(\prime)(x)=(4)/(4x+1)+3-2x \\ \\ Pu\text{t x = 0.9} \\ \\ P^(\prime)(0.9)=(4)/(4(0.9)+1)+3-2(0.9) \\ \\ P^(\prime)(0.9)=(238)/(115) \\ \\ P^(\prime)(0.9)=2.069565217 \\ \\ P^(\prime)(0.9)=2.07million\text{ }dollars\text{ }per\text{ }thosandemployees \end{gathered}`

Therefore, the answer is

`2.07million\text{ }dollars\text{ }per\text{ }thosand\text{ }employees`