Question

A vehide factory manufactures cars. The unit cost C (the cost in dollars to make each car) depends on the number of cars made. If u cars are made, then theunit cost is given by the function C(x)=1.1x^2638x+103,259. What is the minimum unit cost?Do not round your answer.

Answer 1

The cost function is given as,

`C(x)=1.1x^2-638x+103259`

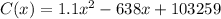
Obtain the first derivative as,

`C^(\prime)(x)=1.1(2x)-638(1)=2.2x-638`

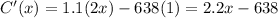
Obtain the critical points by equating the first derivative to zero,

`C^(\prime)(x)=0\Rightarrow2.2x-638=0\Rightarrow2.2x=638\Rightarrow x=290`

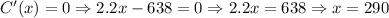
Thus, the Cost function has an extrema at point 290.

Apply the second derivative test,

`C^(\doubleprime)(x)=(d \square)/(dx)(2.2x-638)=2.2`

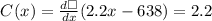
Since the second derivative is positive, the function attains minimum value at the critical point.

Therefore, it is concluded that the cost is minimum at 290.

Substitute the value in the function to obtain the minimum cost,

`C_(\min )=C(290)=1.1(290)^2-638(290)+103259=10749`

Thus, the minimum unit cost is $10749 which corresponds to 290 units of cars.