According to the information given in the exercise:
• The cost of admission for couples is $12 and $7 for singles.
,
• On Friday the total amount of money for admissions was $2706.
,
• On Friday a total number of 268 people attended.
Knowing this, you can set up the following System of Equations, where "c" is the number of couples at the dance club on Friday night and "s" is the number of singles at the dance club on Friday night.
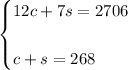
You can use the Elimination Method in order to find the value of "s":
1. Multiply the second equation by -12:

2. Add the equations:
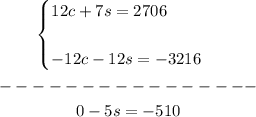
3. Solve for "s":
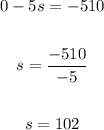
Therefore, the answer is: There were 102 singles.