Question

Find the exact value of cos θ if sinθ=1/4 , 90°< θ < 180°

Answer 1

We have to calculate the cosine of an angle using the value of its sine. For this purpose we can use the following relation that is met for any angle:

`\sin ^2\theta+\cos ^2\theta=1`

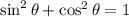
Then, the cosine is given by:

`\begin{gathered} \sin ^2\theta+\cos ^2\theta=1 \\ \cos ^2\theta=1-\sin ^2\theta \\ \cos \theta=\sqrt[]{1-\sin^2\theta} \\ \lvert\cos \theta\rvert=\sqrt[]{1-((1)/(4))^2}=\sqrt[]{1-(1)/(16)}=\sqrt[]{(15)/(16)} \end{gathered}`

This means that the cosine is either:

`\sqrt[]{(15)/(16)}`

or:

`-\sqrt[]{(15)/(16)}`

Since the angle theta is between 90° and 180° then its cosine must be a negative number then:

`\cos \theta=-\sqrt[]{(15)/(16)}`