Question

A rectangular carport has area 150 square feet. The height of the carport is five feet less than twice its length. Find the height and the length of the carport.

Answer 1

We are given that the area of a rectangle is 150 square feet. If "h" is the height and "l" is the length then the area is given by:

`hl=150`

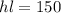
We are also given that the height is 5 feet less than twice its length, this can be written mathematically as:

`h=2l-5`

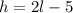
Now we can replace the value of "h" in the equation for the area:

`(2l-5)l=150`

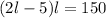
Now we use the distributive property:

`2l^2-5l=150`

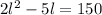
Now we have a quadratic equation that can be written as:

`2l^2-5l-150=0`

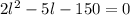
We can factor this equation to determine the values of "l". We multiply and divide by 2:

`(4l^2-5(2l)-300)/(2)=0`

Factoring in the numerator:

`((2l-20)(2l+15))/(2)=0`

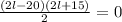
Now we take common factor in the first parenthesis in the numerator:

`(2(l-10)(2l+15))/(2)=0`

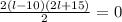
Simplifying:

`(l-10)(2l+15)=0`

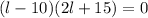
Now we set each factor to zero:

`\begin{gathered} l_1-10=0 \\ l_1=10 \\ 2l_2+15=0 \\ l_2=-(15)/(2) \end{gathered}`

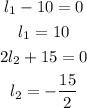
We take the positive value, therefore, the length of the rectangle is 10 feet. Now we replace this value in the equation for the height.

`h=2(10)-5`

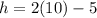
Solving we get:

`\begin{gathered} h=20-5 \\ h=15 \end{gathered}`

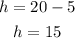
Therefore, the height of the rectangle is 15 feet.