Question

Triangle jkl is similar to Triangle jkl find the length of segment JK I'll send you the picture

Answer 1

Two triangles that are similar have the following characteristics:

1) The corresponding angles are congruent

2) The corresponding sides ratios have the same proportion.

So for triangles, JKL and J'K'L' the ratios of the corresponding sides are:

`(J^(\prime)K^(\prime))/(JK)=(K^(\prime)L^(\prime))/(KL)=(J^(\prime)L^(\prime))/(JL)`

Given

JK=10cm

KL=30cm

K'L'=13.5cm

We can calculate the length of J'K' using the ratios:

`\begin{gathered} (K^(\prime)L^(\prime))/(KL)=(J^(\prime)K^(\prime))/(JK) \\ (13.5)/(30)=(x)/(10) \\ ((13.5)/(30))\cdot10=x \\ x=4.5 \end{gathered}`

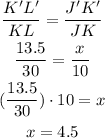
Segment J'K'=4.5cm