The canonical form of the line equation is:
y = mx + b
where m is the slope of the line and b is the intercept with the y-axis.
First, let's find the slope of the line. By definition, the slope of the line is:
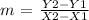
where (X1,Y1) and (X2,Y2) are points on the line. In our case, we have that:
(X1, Y1) = (6,4)
(X2,Y2) = (4,1)
then, the slope of the line will be:
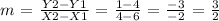
Then, for now, we have the following line equation:
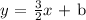
Now, we are going to find the y-intercept (b). For this purpose, we will take any of the given points and replace them in the previous equation. Then we will solve for b. In our case, we take the point (4,1) = (x,y):
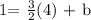
That is equivalent to:
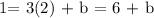
that is
1 = 6 + b
now, we resolve for b
b = 1-6 = -5.
Then the y-intercept is -5. Then, we can conclude that the line equation is
