Question

What is the y coordinate of the center of the circle and the value of b in the equation?

Answer 1

We are given the following equation of a circle.

`x^2+y^2-6x+4y=b`

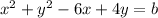
Recall that the standard form of the equation of a circle is given by

`(x-h)^2+(y-k)^2=r^2`

Where (h, k) are the coordinates of the center and r is the radius of the circle.

Let us convert the given equation into the standard form to find out the coordinates of the center.

We can use completing the square method for the conversion.

`\begin{gathered} x^2+y^2-6x+4y=b \\ x^2-6x+y^2+4y=b \\ x^2-6x+(-(6)/(2))^2+y^2+4y+((4)/(2))^2=b+(-(6)/(2))^2+((4)/(2))^2 \\ x^2-6x+(-3)^2+y^2+4y+(2)^2=b+(-3)^2+(2)^2 \\ x^2-6x+9^{}+y^2+4y+4^{}=b+9+4 \\ (x^2-6x+9)^{}+(y^2+4y+4)^{}=b+13 \\ (x^{}-3)^2+(y^{}+2)^2=b+13 \end{gathered}`

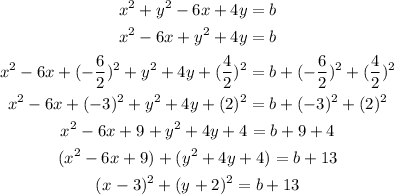
So, the coordinates of the center are

`(h,k)=(3,-2)`

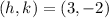
Therefore, the y-coordinate of the center is -2

Since the radius of the circle is 10

`\begin{gathered} r^2=10^2=100 \\ r^2=b+13 \\ 100=b+13 \\ b=100-13 \\ b=87 \end{gathered}`

Therefore, the value of b is 87