Solution:
The area of the sector of a circle is expressed as
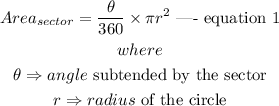
Given that the area of the sector of the circle is 23.2 square inches, and the diameter of the circle is 24 inches, to calculate the missing degree of the sector,
step 1: Evaluate the radius r of the circle.
The radius of the circle is expressed as
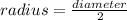
Thus, the radius of the circle is evaluated to be

step 2: Substitute the parameters (area of sector, radius of circle) into equation 1.
Thus, from equation 1
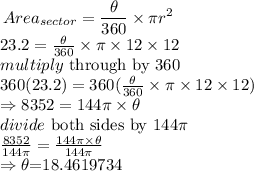
Hence, the value of the missing degree of the sector is 18.4619734°.