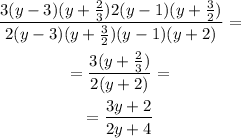Question

Divide the rational expressions and express in simplest form. When typing your answer for the numerator and denominator be sure to type the term with the variable first with no spaces between characters.\frac{\left(3y^2-7y-6\right)}{\left(2y^2-3y-9\right)}\div \frac{\left(y^2+y-2\right)}{\left(2y^2+y-3\right)}The numerator is AnswerThe denominator is Answer

Answer 1

Dividing by a fraction is equivalent to multiply by its reciprocal, then:

`\begin{gathered} (3y^2-7y-6)/(2y^2-3y-9)/\frac{y^2+y-2}{2y^2+y-3^{}}= \\ =(3y^2-7y-6)/(2y^2-3y-9)\cdot(2y^2+y-3)/(y^2+y-2)= \\ =((3y^2-7y-6)(2y^2+y-3))/((2y^2-3y-9)(y^2+y-2)) \end{gathered}`

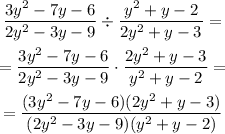
Now, we need to express the quadratic polynomials using their roots, as follows:

`ay^2+by+c=a(y-y_1)(y-y_2)`

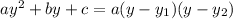
where y1 and y2 are the roots.

Applying the quadratic formula to the first polynomial:

`\begin{gathered} y_(1,2)=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a} \\ y_(1,2)=\frac{7\pm\sqrt[]{(-7)^2-4\cdot3\cdot(-6)}}{2\cdot3} \\ y_(1,2)=\frac{7\pm\sqrt[]{121}}{6} \\ y_1=(7+11)/(6)=3 \\ y_2=(7-11)/(6)=-(2)/(3) \end{gathered}`

Applying the quadratic formula to the second polynomial:

`\begin{gathered} y_(1,2)=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a} \\ y_(1,2)=\frac{-1\pm\sqrt[]{1^2-4\cdot2\cdot(-3)}}{2\cdot2} \\ y_(1,2)=\frac{-1\pm\sqrt[]{25}}{4} \\ y_1=(-1+5)/(4)=1 \\ y_2=(-1-5)/(4)=-(3)/(2) \end{gathered}`

Applying the quadratic formula to the third polynomial:

`\begin{gathered} y_(1,2)=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a} \\ y_(1,2)=\frac{3\pm\sqrt[]{(-3)^2-4\cdot2\cdot(-9)}}{2\cdot2} \\ y_(1,2)=\frac{3\pm\sqrt[]{81}}{4} \\ y_1=(3+9)/(4)=3 \\ y_2=(3-9)/(4)=-(3)/(2) \end{gathered}`

Applying the quadratic formula to the fourth polynomial:

`\begin{gathered} y_(1,2)=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a} \\ y_(1,2)=\frac{-1\pm\sqrt[]{1^2-4\cdot1\cdot(-2)}}{2\cdot1} \\ y_(1,2)=\frac{-1\pm\sqrt[]{9}}{2} \\ y_1=(-1+3)/(2)=1 \\ y_2=(-1-3)/(2)=-2 \end{gathered}`

Substituting into the rational expression and simplifying:

`\begin{gathered} (3(y-3)(y+(2)/(3))2(y-1)(y+(3)/(2)))/(2(y-3)(y+(3)/(2))(y-1)(y+2))= \\ =(3(y+(2)/(3)))/(2(y+2))= \\ =(3y+2)/(2y+4) \end{gathered}`