Remember that the steps to solve a system of linear equations (2x2) are:
0. Arrange the equations with like terms in columns.
,
1. Analyze the coefficients of x or y, and try to eliminate one.
,
2. Add the equations and solve for the remaining variable.
,
3. Substitute the value into either equation and solve.
Notice that if we multiply equation 1 by -2 and add it up with equation 2, we'll eliminate x , as following:
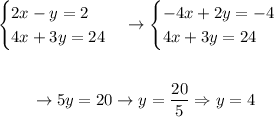
Now, we plug in this value in equation 2 and solve for x :
