Question

What is the length of SQ?

Answer 1

In the given triangles RTS and PTQ

Angle RTS = Angle PTQ (Common Angle)

Agle SRT = Angle QPT (Corresponding angle)

Thus, from Angle Angle similarity, triangle RTS and PTQ are similar

From the properties of similar triangle, The ratio of corresponding sides of the similar triangle always equal:

`(RT)/(PT)=(TS)/(TQ)=(SR)/(QP)`

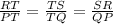
In the given figure :

RT = RP + PT

RT = 2 + 18

RT = 20

Substitute each value and simplify :

`\begin{gathered} (RT)/(PT)=(TS)/(TQ)=(SR)/(QP) \\ (20)/(18)=(TS)/(27)=(SR)/(QP) \\ Simplify\text{ the first two expression :} \\ (20)/(18)=(TS)/(27) \\ TS\text{ = }(20*27)/(18) \\ TS=(10*27)/(9) \\ TS=(10*3)/(1) \\ TS=30 \end{gathered}`

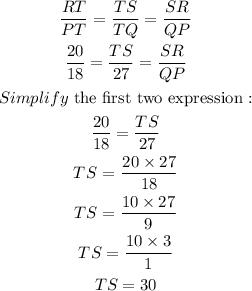
As TS = TQ + QS

30 = 27 + SQ

SQ = 30 - 27

SQ = 3

Answer : C) 3 cm