Question

An 8-sided die with faces labeled 1 to 8 will be rolled once. The 8 possible outcomes are listed below. Note that each outcome has the same probability. Complete parts (a) through (C). Write the probabilities as fractions. (a) Check the outcomes for each event below. Then, enter the probability of the event. Outcomes Probability 1 2. 3 4 5 6 7 00 Event A: Rolling a number greater than 4 Event B: Rolling an even number o Event A and B: Rolling a number greater than 4 and rolling an even number Event A or B: Rolling a number greater than 4 or rolling an [ ( [ [ Continue

Answer 1

1i) P(A) = 1/2

ii) P(B) = 1/2

iii) P(A and B) = 1/4

2) P(A) + P(B) - P(A and B) = 3/4

3) P(A or B)/ P(A U B)

Explanations:

Probability is the likelihood or chance that an event will occur. Mathematically;

`\text{Probability}=(n(E))/(n(S))`

n(E) is the number of events

n(S) is the total sample space

An 8-sided die with faces labeled 1 to 8 will be rolled once, the sample space will be S = {1, 2, 3, 4, 5, 6, 7, 8}

n(S) = 8

a i) For event A, we need to get the number of outcome greater than 4.

A = {5, 6, 7, 8}

n(A) = 4

P(A) = n(A)/n(S)

P(A) = 4/8 = 1/2

ii) For event B, we need the outcomes that gives an even number.

B = {2, 4, 6, 8}

n(B) = 3

P(B) = n(B)/n(S)

P(B) = 4/8 = 1/2

iii) For the probability of the event of rolling a number greater than 4 and rolling an even number,

P(A and B) = P(A) * P(B)

P(A and B) = 1/2 * 1/2

P(A and B) = 1/4

2) To compute P(A) + P(B) - P(A and B), we will substitute resulting probabilities in (a) into the expression as shown:

`\begin{gathered} \text{ P(A)+ P(B) - P(A and B) } \\ \text{= }(1)/(2)+(1)/(2)-(1)/(4) \\ =(2+2-1)/(4) \\ =(3)/(4) \\ \end{gathered}`

Hence P(A) + P(B) - P(A and B) = 3/4

3) Note that P(A and B) can also be written as P(A n B) and according to set theory;

`P(A\cup B)=P(A)+P(B)-P(A\cap B)`

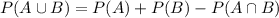
This can be also be expressed as:

`\text{ P(A or B) = P(A) + P(B) -P(A and B)}`

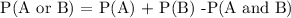
Hence from these two notations, we can see that the answer that makes the equation true is P(A or B)/P(A U B)