Question

Write a equation to find the nth term of each sequence -4, -9, -14, -19. Then find the a24

Answer 1

Given an arithmetic sequence like the one in the question with "a" being the 1st term and "d" being the common difference, the equation to find the nth term of the sequence can be written thus;

`a_n=a+(n-1)d`

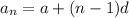
In the question, we've also been asked to find the 24th term of the sequence.

To do that, we need to substitute the values of the variables a, n and d into the above equation.

From the sequence -4, -9, -14, -19, the 1st term(a) is -4, the common difference is -5 and n = 24.

Let's substitute and find the 24th term of the sequence;

`\begin{gathered} a_(24)=-4+(24-1)(-5)_{}_{} \\ =-4+(23)(-5) \\ =-4-115 \\ =-119 \end{gathered}`

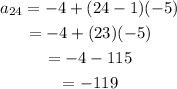
Therefore, the 24th term of the sequence is -119.