Question

An isosceles triangle has a vertex angle of 21.21°. Two sides of the triangle are each 17.91 ft long. Find the area of the triangle.A. 160.384 sq ftB. 49.314 sq ftC. 58.025 sq ftD. 60.025 sq ft

Answer 1

To calculate the area of a triangle with two sides given and the angle opposite the third side, we shall apply the following formula;

`\begin{gathered} \text{Area}=ab*(\sin C)/(2) \\ \text{Where} \\ a=\text{side,b}=\text{side,C}=\text{angle} \end{gathered}`

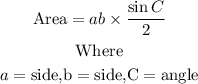
The triangle is an isosceles triangle, which mean sides a and b both measure 17.91 ft each and angle C = 21.21 degrees.

Therefore, the area would be;

`\begin{gathered} \text{Area}=17.91*17.91*(\sin 21.21)/(2) \\ \text{Area}=320.7681*(0.361787285773668)/(2) \\ \text{Area}=320.7681*0.180893642886834 \\ \text{Area}=58.023625\ldots \\ \text{Area}\approx58.024ft^2\text{ (rounded up to the nearest thousandth)} \end{gathered}`

The correct answer therefore is option C, which is 58.025 sq ft.

This is the closest we got from our calculation which is as a result of approximations