Question

A harmonic wave on a string is described by

Y (x, t) = 0.1 sin (300t +0.01x + л/3) mm, where x is in cm and t is in seconds.

a) Does the wave represent a travelling wave or a standing wave?
b) What is the direction of its propagation?
c) What is its period?
d) What is its wavelength?
e) What is the amplitude of the particle?

Answer 1

`\huge{\bold{\orange{\underline{ Solution }}}}`

Given :-

A harmonic wave on a string is described by

`\sf{ Y( x, t) = 0.1 sin(300t + 0.01x + π/3)}`

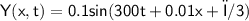
• x is in cm and t is in seconds

Answer 1 :-

Equation for travelling wave :-

`\sf{ Y( x, t) = Asin(ωt + kx + Φ)...eq(1)}`

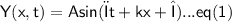
Equation for stationary wave :-

`\sf{ Y( x, t) = Acos(ωt - kx )...eq(2)}`

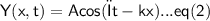
Given equation for wave :-

`\sf{ Y( x, t) = 0.1 \:sin(300t + 0.01x + π/3)...eq(3)}`

On comparing eq(1) , (2) and (3)

We can conclude that, Given wave represent travelling wave.

Answer 2 :-

From solution 1 , We can say that,

`\sf{ Y( x, t) = 0.1 \: sin(300t + 0.01x + π/3).}`

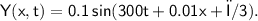
It is travelling from right to left direction

Hence, The direction of its propagation is right to left that is towards +x direction.

Answer 3 :-

Here, We have to find the wave period

We know that,

Wave period = wavelength / velocity

Wave equation :-

`\sf{ Y( x, t) = 0.1 \:sin(300t + 0.01x + π/3).}`

• ω = 300rad/s
• k = 0.01

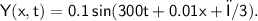
We know that,

`\sf{v =}{\sf{( ω)/(2π)}}{\sf{\: and\:}}{\sf{ λ =}}{\sf{( 2π)/(k)}}`

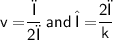
Subsitute the required values,

`\sf{ wave\: period =}{\sf{( 2π/k)/(ω/2π )}}`

`\sf{ wave \:period = }{\sf{(k)/(ω)}}`

`\sf{ wave\: period =}{\sf{( 0.01)/(300)}}`

`\sf{ wave\: period = 0.000033\: s}`

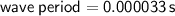
Answer 4 :-

The wavelength of given wave

`\bold{ λ = }{\bold{(2π)/(k)}}`

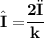
Subsitute the required values,

`\sf{ λ = }{\sf{(2 × 3.14 )/(0.01)}}`

`\sf{ λ = }{\sf{(6.28)/(0.01)}}`

`\sf{ λ = 628 \: cm }`

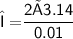
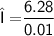
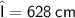
Answer 5 :-

We have wave equation

`\sf{ Y( x, t) = 0.1 sin(300t + 0.01x + π/3).}`

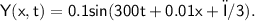
Travelling wave equation :-

`\sf{ Y( x, t) = A\:sin(ωt + kx + Φ)...eq(1)}`

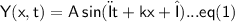
Therefore,

Amplitude of the wave particle

`\sf{ A = 0.1 \: cm}`

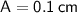
Hence, The amplitude of the particle is 0.1 cm