Question

What is the sum of the geometric series, rounded to the nearest whole number?See image

Answer 1

The formula of the partial sum of the first n terms of a geometric series is:

`Sn=(a1(1-r^n))/(1-r)`

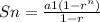
In this case, a1 is 6 (the first term of the series) and r is 1/4 (the base). By replacing 16 for n and the rest of the values we should get:

`Sn=(6(1-((1)/(4))^(16)))/(1-((1)/(4)))\approx8`

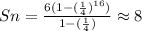
Then, the sum of the given geometric series is 8