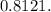Question

An insurance company prices its Tornado Insurance using the following assumptions:• In any calendar year, there can be at most one tornado.• In any calendar year, the probability of a tornado is 0.08.• The number of tornadoes in any calendar year is independent of the number of tornados in any othercalendar year.Using the insurance company's assumptions, calculate the probability that there are fewer than 2 tornadoes in a10-year period. Round your answer to four decimal places.PreviewTIP

Answer 1

To answer this question we will use the following formula for binomial probability:

`P(x)={\binom{n}{x}}p^xq^(n-x),`

where x is the number of times for a specific outcome within n trials, p is the probability of success on a single trial, q is the probability of failure on a single trial, and n is the number of trials.

Now, notice that:

`P(x<2)=P(0)+P(1)\text{.}`

Substituing x=0, p=0.08, q=0.92, and n=10 in the formula we get that:

`P(0)={\binom{10}{0}(0.08)^0}(0.92)^(10-0)\text{.}`

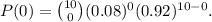
Simplifying the above result we get:

`\begin{gathered} P(0)=(10!)/((10-0)!0!)(0.08)^0(0.92)^(10) \\ =0.92^(10)\text{.} \end{gathered}`

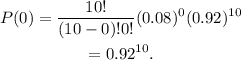
Substituting x=1, p=0.08, q=0.92, and n=10 in the formula we get that:

`P(1)={\binom{10}{1}(0.08)^1}(0.92)^(10-1)\text{.}`

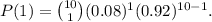
Simplifying the above result we get:

`\begin{gathered} P(1)=(10!)/((10-1)!1!)(0.08)^1(0.92)^9 \\ =10\cdot0.08\cdot0.92^9\text{.} \end{gathered}`

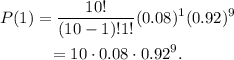
Therefore:

`\begin{gathered} P(x<2)=0.92^(10)+0.8\cdot0.92^9 \\ \approx0.8121. \end{gathered}`

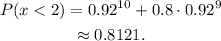
Answer:

`0.8121.`