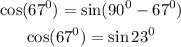Question

The figure below is a right triangle with side lengths t, u, and v.Suppose that m

Answer 1

Using trigonometry ratios SOH, CAH, TOA

Opposite (O) is the side facing the chosen angle, Adjacent is the side that is adjacent to the opposite side, and Hypothenuse (H) is the longest side facing the right angle

`\begin{gathered} \sin =\frac{opposite}{\text{hypothenuse}} \\ \cos =\frac{adjacent}{\text{hypothenuse}} \\ \tan =\frac{opposite}{\text{adjacent}} \end{gathered}`

From the given right-angled triangle, with reference angle T

`\begin{gathered} \sin T=\frac{opposite}{\text{hypothenuse}}=(t)/(v) \\ \cos T=\frac{adjacent}{\text{hypothenuse}}=(u)/(v) \end{gathered}`

`\begin{gathered} \cos U=(t)/(v) \\ \sin U=(u)/(v) \end{gathered}`

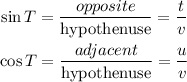
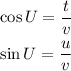
Part 2:

`\Delta TUV,\angle Tand\angle U\text{ are complementary}`

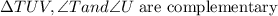
Complementary angles are angles that add up to 90°

`\begin{gathered} \angle T+\angle U+\angle V=180^0 \\ \angle V=90^0 \\ \angle T+\angle U+90^0=180^0 \\ \angle T+\angle U=180^0-90^0 \\ \angle T+\angle U=90^0 \end{gathered}`

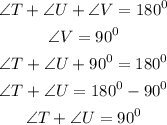
Since Part 3

From the trigonometric ratios gotten earlier above, it can be seen that

`\begin{gathered} \sin T=\cos U=(t)/(v) \\ \cos T=\sin U=(u)/(v) \end{gathered}`

The second and the third options are true statements

`\begin{gathered} \angle T+\angle U=90^0 \\ \angle T=90^0-\angle U;\angle U=90^0-\angle T \\ \sin T=\cos (90-\angle T) \\ \cos T=\sin (90-\angle T) \end{gathered}`

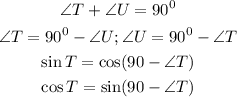
Part 4

`\begin{gathered} \cos (67^0)=\sin (90^0-67^0) \\ \cos (67^0)=\sin 23^0 \end{gathered}`