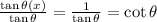ANSWER :
d. cot θ
EXPLANATION :
Note that the reciprocal of tangent is cotangent.
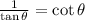
If reciprocals are multiplied with each other, the result is 1.
From the problem, we have :

Since the result of the product is 1, the tangent function must be multiplied by its reciprocal.
That will be cotangent.
Or we can just simply divide the equation by tan θ.