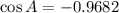Question

Suppose sin(A) = 1/4 Use the trig identity sin^2(A)+cos^2(A)=1 to find the cosine in quadrant II. round to ten-thousandth.0.1397-0.9682-0.85720.4630

Answer 1

To find the value f rthe cosine function we will us the identity:

`\sin^2A+\cos^2A=1`

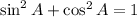
We know that the sine of A i 1/4 then we have:

`\begin{gathered} ((1)/(4))^2+\cos^2A=1 \\ \cos^2A=1-(1)/(16) \\ \cos A=\pm\sqrt{(15)/(16)} \\ \cos A=\pm0.9682 \end{gathered}`

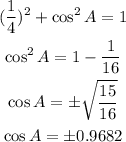
Now, we need to determine which sign to choose. Since the sinA lies in th second quadrant thismeans that tehe coosine als lies in the quadrant; furthermore, we know that the cosine is negative in the second and thirsd quadrants whichmeans that we need to use the negative sign. Therefoore:

`\cos A=-0.9682`