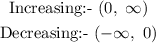Y=5x^2 + 2find the minimum or maximum value of the function. describe the domain and range of the function, and where the function is increasing and decreasing.I'm not sure…

Question

asked Dec 4, 2023 99.2k views

1 Answer

Nedned · Answer 1 · 2023-12-09T02:05:25+0000

From the given equation,

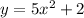
Now,

For find the maximum and minimum value of the function,

The maximum and minimum of the function is,

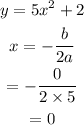
$\begin{gathered} y=5x^2+2 \\ x=-(b)/(2a) \\ =-(0)/(2*5) \\ =0 \end{gathered}$

Then,

Put the value of x into the given equation to find the value of y,

So;

$\begin{gathered} y=5(0)^2+2 \\ y=0+2 \\ y=2 \end{gathered}$

Hence, the maximum and minimum function is,

(0, 2).

Now,

The domain of the given funcytion is,

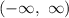
$(-\infty,\text{ }\infty)$

And,

The range of the given function is,

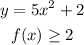
$\begin{gathered} y=5x^2+2 \\ f(x)\ge2 \end{gathered}$

So,

The range of function is,

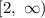
$\lbrack2,\text{ }\infty)$

The increasing and decreasing of the function is,

$\begin{gathered} \text{Increasing:- }(0,\text{ }\infty) \\ \text{Decreasing:- }(-\infty,\text{ 0)} \end{gathered}$