Given the two inequalities below,
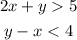
We will have to start substituting all the coordinates given to obtain the solution to the system of linear inequalities.
Checking
Option A
(3,1)
Where x = 3, y = 1

The coordinates satisfy the first inequality, let us now check the second inequality
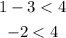
It also satisfies the second inequality, so therefore (3,1) is a solution to the inequality.
Option B
(4.5, 0)
Where x =4.5, y = 0
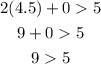
The coordinates satisfy the first inequality, let us now check the second inequality
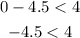
This also satisfies the two inequalities but since 4.5 is not an integer, therefore (4.5 , 0) is not a solution to the system of linear inequalities.
Option C
(-2,1)
Where x = -2, y = 1

Since -3 is not greater than 5. Therefore, (-2,1) is not a solution to the system of linear inequalities.
Option D
(-3,-1)
Where x = -3, y = -1
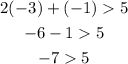
Since -7 is not greater than 5. Therefore, (-3,-1) is not a solution to the system of linear inequalities.
Hence, the solution to the system of linear inequalities is (3,1).
The correct answer is Option A.