Question

Use Part I of the Fundamental Theorem of Calculus to find the derivative of the function

Answer 1

First of all, remember that:

The part I of the Fundamental Theorem of Calculus states that, given a function F of the form:

`F(x)=\int ^x_af(t)dt`

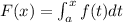
The deritative of this function, is given by:

`F^(\prime)(x)=(d)/(dx)\int ^x_af(t)dt=f(x)`

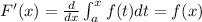
This basically means that the deritative of the function when the integral goes from "a" to "x" can be found just replacing the variable "t" of the function inside the integral by "x". So, in our problem this is:

`\begin{gathered} F(x)=\int ^x_(10)(1)/(9)(t^2+\sqrt[]{t})dt \\ \\ F^(\prime)(x)=(d)/(dx)\int ^x_(10)(1)/(9)(t^2+\sqrt[]{t})dt \\ \\ F^(\prime)(x)=(1)/(9)(x^2+\sqrt[]{x}) \end{gathered}`