Question

I need to find the inverse of this equation but i’m stuck on the fraction (x is in denominator)

Answer 1

The function is given as,

`y=(3)/(4x)-8`

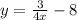
In order to determine the inverse of the function, first, we need to switch the variables 'x' and 'y' in the given equation. And then transform the equation to obtain the form y=f(x).

After switching the variables, the equation becomes,

`x=(3)/(4y)-8`

Now, convert the equation in the form y=f(x) by transposing the terms.

Add 8 on both sides,

`\begin{gathered} x+8=(3)/(4y)-8+8 \\ x+8=(3)/(4y) \end{gathered}`

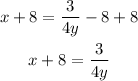
Multiply the equation by 4/3 as follows,

`\begin{gathered} (x+8)\cdot(4)/(3)=((3)/(4y))\cdot(4)/(3) \\ (4)/(3)x+((8\cdot4)/(3))=(3\cdot4)/(4y\cdot3) \\ (4)/(3)x+(32)/(3)=(1)/(y) \\ (4x+32)/(3)=(1)/(y) \\ (4x+32)/(3)=(1)/(y) \end{gathered}`

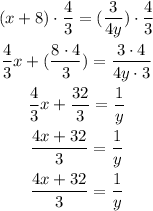
Cross multiply the terms,

`y=(3)/(4x+32)`

Now that the function is converted into the desired form, it can be concluded that the inverse is obtained.

Therefore, the required inverse function is obtained as,

`y=(3)/(4x+32)`