Question

And draw the tangent lines to the graph at points whose x-coordinates are -2 , 0, and 1.

Answer 1

a)

To find the difference quotient we will do

`(f(x+h)-f(x))/(h)`

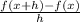
But f(x) = 4x, therefore f(x+h) = 4(x+h). Then

`(f(x+h)-f(x))/(h)=(4(x+h)-4x)/(h)`

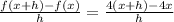
Now we just simplify the expression

`(4(x+h)-4x)/(h)=(4x+4h-4x)/(h)=(4h)/(h)=4`

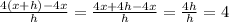
Therefore

`(f(x+h)-f(x))/(h)=4`

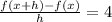
As expected, because the function f is a linear function, then it must be a constant.

b)

As we can see we don't have the term "h" in the difference quotient, then we can easily solve the limit by just repeating the result:

`\lim _(h\rightarrow0)(f(x+h)-f(x))/(h)=\lim _(h\rightarrow0)4=4`

Therefore

`f^(\prime)(x)=4`

See that it's a constant function, it means that the slope will always be the same, doesn't matter the value of x.