Solution
Part C
From the figure, each sides of both triangle are:
Triangle ABC
![\begin{gathered} AB\text{ = 3} \\ BC\text{ = 3} \\ AC\text{ = }\sqrt[]{AB^2+BC^2} \\ AC\text{ = }\sqrt[]{3^2+3^2} \\ AC\text{ = }\sqrt[]{9\text{ + 9}}\text{ = }\sqrt[]{18\text{ }}\text{ = 3}\sqrt[]{2} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/la4q922wdgk1qowa4tgt368nnw9ainnm4z.png)
![\begin{gathered} \text{From the triangle ABC} \\ \text{Opposite = 3} \\ \text{Adjacent = 3} \\ \text{Hypotenuse = 3}\sqrt[]{2} \\ \angle ABC\text{ = 90} \\ \angle ACB\text{ = 45} \\ \angle BAC\text{ = 45} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/skqvk9pbkx2nq0qw6to9pn5s64r9bys3h4.png)
Next
For triangle DEF
DE = 6
EF = 6
DF = ?
![\begin{gathered} \text{Apply the pythagoras theorem} \\ DF\text{ = }\sqrt[]{DE^2+EF^2} \\ DF\text{ = }\sqrt[]{6^2+6^2} \\ DF\text{ = }\sqrt[]{36+36}\text{ = }\sqrt[]{72}\text{ = 6}\sqrt[]{2} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/92lq16m3foo8cvrejinvo4p4u835nue8xj.png)
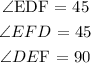
Part D
The two lengths have been increased by a scale factor of 2. The corresponding angle is the same.
Two triangles are similar if the angles are the same size or the corresponding sides are in the same ratio. Either of these conditions will prove two triangles are similar.
The two triangles are similar with SSS in the same proportion (side side side) All three pairs of corresponding sides are in the same proportion.
Triangle ABC is increased by a scale factor of 2 to triangle DEF.