Question

Which cannot be the lengths of the sides of a given triangle? A. 12 m, 8 m, and 14 m O B. 12 m, 8 m, and 20 m O C. 8 m, 9 m, and 16 m O D. 8 m, 13 m, and 20 m

Answer 1

To determine which set of lengths of the sides cannot be of a given triangle you have to apply the triangle inequality theorem.

This theorem states that the sum of any two sides of a triangle must be greater than the length of the third triangle.

For each set of sides, you have to prove if the theorem applies or not.

A. 12m, 8m, and 14m

`\begin{gathered} 12+8>14 \\ 20>14 \end{gathered}`
`\begin{gathered} 12+14>8 \\ 26>8 \end{gathered}`
`\begin{gathered} 14+8>12 \\ 22>12 \end{gathered}`

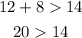
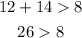
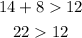
These side lengths meet the conditions to be the sides of a triangle.

B. 12m, 8m, and 20m

`\begin{gathered} 12+8>20 \\ 20>20 \end{gathered}`

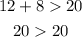
→ This statement is false, 20 cannot be greater than 20

`\begin{gathered} 12+20>8 \\ 32>8 \end{gathered}`

→This result checks

`\begin{gathered} 8+20>12 \\ 28>12 \end{gathered}`

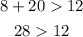
→This result checks

These side lengths do not meet the conditions to be the sides of a triangle

C. 8m, 9m, and 16m

`\begin{gathered} 8+9>16 \\ 17>16 \end{gathered}`

→This result checks

`\begin{gathered} 8+16>9 \\ 24>9 \end{gathered}`

→This result checks

`\begin{gathered} 9+16>8 \\ 25>8 \end{gathered}`

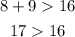
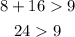
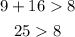
→This result checks

D.8m, 13m, and 20m

`\begin{gathered} 8+13>20 \\ 21>20 \end{gathered}`

→This result checks

`\begin{gathered} 8+20>13 \\ 28>13 \end{gathered}`

→This result checks

`\begin{gathered} 13+20>8 \\ 26>8 \end{gathered}`

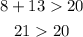
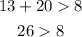
→This result checks

The only set of lengths of sides that cannot correspond to a given triangle is B. 12m, 8m, 20m