We have

We will use the next properties
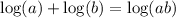
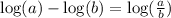
Then we apply the properties
Here we use the first property two simplify the first two terms
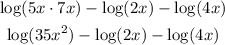
Here we use the second property to simplify the first three terms
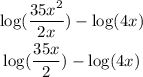
Here we use the second property to simplify the whole expression
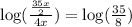
ANSWER
log(35/8)