Given the question in the image, the following are the solution to the questions:
a. null hypothesis
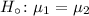
alternative hypothesis
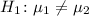
Question b: To get the test statistic, t
![\begin{gathered} t=\frac{(X_1-X_(2))-(\mu_1-\mu_2)_{}_{}}{\sqrt[\square]{(s_(1^2))/(n_1)-(s_(2^2))/(n_2)_{}}} \\ \text{Since }\mu_1=\mu_(2,)difference=0 \\ t=\frac{(27.1141-26.3239)}{\sqrt[\square]{(7.687374^2)/(50)+(5.039494^2)/(50)}} \\ t=\frac{0.7902}{\sqrt[\square]{1.18191-0.50793}} \\ t=(0.7902)/(0.67398) \\ t=1.1724 \\ t\approx1.17 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/6i4oh9o8e5mn6143kgkb0hl4vicf2jj936.png)
Question c: To get the P-value from T score with 0.05 significance level and two tailed hypotheses:

Question d: Conclusion for the test:
Since the P-value is greater than the significance level (0.05), then the correct option is C. Fail to reject the null hypothesis. There is not sufficient evidence to warrant rejection of the claim that men and women have the same mean BMI.
Question e: