Given the function

The second derivative of the function is obtained as
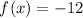
Since the f''(x) is negative, the function has a maxima.
At the critical point, f'(x)=0. Thus,
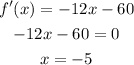
Substitute the value of x in the function, to obtain y.
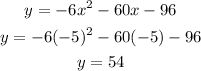
Thus, we obtain a relative maxima at (-5,54)
There is no relative minimum.