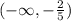From the present question, we have the following inequality to solve:
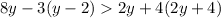
To maintain the inequality unchanged, to every change we make on one of the sides, we MUST make the same on the other. Now, we can verify the simplest way to write the left side of this inequality, as follows:
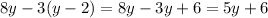
And for the right side, we can make it become the simplest expression as follows:
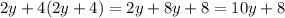
From this, we can rewrite the inequality as:
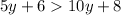
Now, we can subtract both sides with (5y+8), as follows:
From this, we conclude that y can assume any value lower than -2/5. And in interval notation, we write: