Question

A family reunion planning committee with 7 members plans to elect 3 officers, president, vice-president, andtreasurer. If each office is to be held by one person and no person can hold more than one office, in how manyways can those offices be filled?

Answer 1

Concept

The process is a combination which is the selection of r objects out of n objects.

`\begin{gathered} ^{} \\ \text{Number of ways of selecting r objects out of n objects} \\ =^nC_r\text{ = }\frac{n!}{(n\text{ - r)! r!}} \end{gathered}`

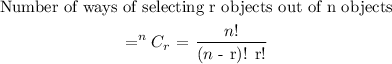
Next,

Given data, you are to select 3 members out of 7 members.

r = 3

n = 7

Substituting n and r into the equation we get a number of ways.

`\begin{gathered} \text{Therefore, } \\ ^{}\text{Number of ways = } \\ =^nC_r \\ =^7C_3 \\ =\text{ }\frac{7!}{(7-3)!\text{ 3!}} \\ =\text{ }\frac{7!}{4!\text{ x 3!}} \end{gathered}`

Next, use your calculator to 7! , 4! and 3!.

`\begin{gathered} =\text{ }\frac{7!}{4!\text{ x 3!}}\text{ = }\frac{5040}{24\text{ x 6}} \\ =\text{ }(5040)/(144) \\ =\text{ 35 ways} \end{gathered}`

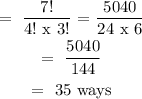
Final answer = 35 ways